Desafío: qué es la paradoja del cumpleaños

¿Cuántas personas se necesitan para estar seguros de que al menos 2 de ellas cumplen años el mismo día? Supongamos adicionalmente que los años siempre tienen 365 días, es decir que nadie puede cumplir años el 29 de febrero. La respuesta es que necesitamos al menos 366 personas para estar completamente seguros de que al menos 2 cumplen el mismo día. Si el grupo es de 365 personas podría darse el improbabilísimo caso de que todas ellas cumplan años en días distintos. Si consideramos los años bisiestos la respuesta sería que hacen falta 367 personas.

Bien, ahora reformulemos la pregunta inicial de la siguiente manera: ¿cuántas personas se necesitan como mínimo para que sea más probable que al menos 2 de ellas cumplan años el mismo día respecto de encontrar que ninguna cumple años el mismo día? Nótese que en la pregunta inicial queremos dar con el número de personas de las que resulte una probabilidad del 100% de satisfacer la condición, mientras que en la segunda pregunta buscamos que esa misma probabilidad sea mayor al 50%.

La situación que plantea esta segunda pregunta se conoce como la paradoja del cumpleaños y establece que (manteniendo el supuesto de que los años tienen 365 días) hacen falta solo 23 personas para que haya una probabilidad de más del 50% de que al menos 2 de ellas cumplan años el mismo día. Obviamente esto no es ninguna paradoja sino un resultado estadístico, sin embargo, su nombre se debe a que el resultado contradice la intuición.

Me voy a saltear la explicación del cálculo (por ahora) y, a continuación, presento una tabla con las probabilidades de satisfacer la condición de que al menos 2 personas cumplan años el mismo día para algunos casos (significativos) con distintas cantidades de personas:

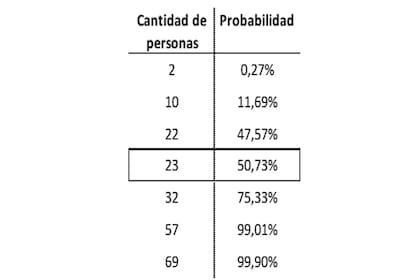
Fíjense que resulta también asombroso que solo se necesiten 57 personas para que la probabilidad sea superior al 99%.

Compartí la paradoja del cumpleaños hace una semana con mi mujer, mis 4 hijos de entre 18 y 11 años y mi sobrina de 12 años, que ya es aficionada a las matemáticas, mientras disfrutábamos de un día de playa en Pinamar. Ante mi sorpresa se mostraron muy interesados. Tanto fue así que conflictuados por la respuesta correcta salieron a preguntar a personas desconocidas de la playa su fecha de cumpleaños. Mi sobrina se ocupó de registrar cuidadosamente en el celular cada fecha de cumpleaños y ante su sorpresa la primera coincidencia se produjo con la persona número 22 que resultó cumplir años el mismo día que la persona número 11, el 10 de mayo. Inmediatamente se preguntaron si en las clases de ellos del colegio de entre 25 y 30 alumnos había al menos 2 que cumplieran el mismo día.

Al día siguiente todavía quisieron entender mejor algo que todavía les seguía resultando extraño. No tuve más remedio que intentar una explicación del cálculo.

Una advertencia: a partir de acá la nota exige otro nivel de concentración por lo que ya me siento satisfecho si se han interesado por esta "curiosidad matemática".

Acá voy con la explicación.

La probabilidad de que un hecho azaroso ocurra está dada por la siguiente fórmula de Laplace que es bastante intuitiva, por cierto:

Dado que los "Casos favorables" son siempre un subconjunto de los "Casos posibles" la probabilidad siempre es un número comprendido entre 0 y 1 siendo 0 una imposibilidad absoluta y 1 una certeza absoluta.

Por otro lado, la probabilidad de que un hecho no ocurra es igual a 1 menos la probabilidad de que ese mismo hecho ocurra.

Por ejemplo, la probabilidad de sacar un 5 al lanzar un dado al aire es 1/6 o el 0,17 o 17%. 1 caso favorable (que salga el 5) dividido entre los 6 casos posibles. A su vez, la probabilidad de que no salga un 5 al lanzar un dado al aire es 1 – 1/6 = 5/6 u 83%.

Con esta introducción volvamos al caso de los cumpleaños. Para facilitar la explicación, supongamos que los años tienen solo 4 días y que queremos determinar cuál es la probabilidad de que, habiendo 3 personas, al menos 2 de ellas cumplan el mismo día. En primer lugar, pensemos la probabilidad contraria a la que estamos buscando, es decir, la probabilidad de que, habiendo 3 personas, ninguna de ellas cumpla el mismo día. La "primera" persona podría cumplir cualquier día y por lo tanto asumiremos que cumple el primer día del año. Con lo cual podríamos reemplazar la probabilidad de que 3 personas no cumplan el mismo día por la probabilidad equivalente de que las otras 2 cumplan en un día distinto a la primera y un día distinto entre sí.

Por lo tanto, los "Casos posibles" son que las 2 personas restantes cumplan el primer día del año y lo podemos representar como 11 o que una de ellas cumpla el primer día y la restante el segundo día: 12 y así buscar todas las posibilidades. A continuación, las enumero:

11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44

Es decir que hay 16 "Casos posibles", o lo que es lo mismo 4 (días por año) elevado a la 2 (las 3 personas del grupo menos 1 que puede cumplir cualquier día).

A su vez, dentro de estos 16 casos debemos elegir aquellos en que cumplan con la condición: que no cumplan el mismo día que la "primera" persona y que no cumplan el mismo día entre sí. Los "Casos favorables" son los 6 subrayados entre los "Casos posibles". Otra forma de calcularlo es la siguiente. Si sabemos que la "primera" persona cumple el día 1, entonces la segunda persona solo podrá cumplir en cualquiera de los 3 días restantes y la última persona en cualquier de los 2 restantes. Por lo tanto, los "Casos favorables" son 3 x 2 = 6.

Es decir que la probabilidad de que habiendo 3 personas 2 de ellas no cumplan el mismo día suponiendo que un año tiene 4 días es de 6/16 = 37,5%. Pero lo que no interesa saber es la probabilidad de que al menos 2 de ellas cumplan el mismo día. Para ello debemos hacer 1 – 37,5% = 62,5%.

Tratemos finalmente de llevar el ejemplo de las 3 personas y el año de 4 días al problema de las 23 personas y nuestro año de 365 días. Tenemos por un lado que los "Casos posibles" son: 365 días por año elevado a la 22. Por otro lado, los "Casos favorables" de que no haya 2 personas que cumplan el mismo día son: 22 x 21 x 20 x…x 2. Por último, si hacemos:

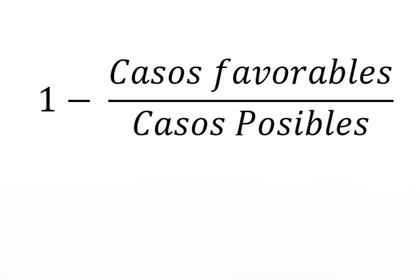
...obtenemos el 50,73% que anticipamos en la tabla.

Por Francisco Ces

• Hoy

---

Conforme a

Vivía en Colegiales. Qué se sabe sobre la muerte de la mujer hallada en un jacuzzi y la pista que siguen del hombre que estaba con ella

A tres años de su desaparición. Comienza el juicio por el caso Tehuel de la Torre

Las fotos de la pasión. Los hinchas argentinos en la previa del partido contra Panamá