¿Cómo puedo saber qué día de la semana cae una fecha dada sin usar un calendario?

El calendario gregoriano tiene varias irregularidades. No todos los meses tienen la misma cantidad de días, no todos los años tienen la misma cantidad de días ya que febrero tiene un día más en los años bisiestos y los años bisiestos no son siempre cada 4 años. Es por ello que, poder deducir un algoritmo o fórmula que nos permita determinar el día de la semana que cayó o caerá una fecha cualquiera tiene cierta complejidad. Por suerte las semanas siempre tienen 7 días y eso nos será de gran ayuda.

Existen distintos algoritmos para calcular qué día de la semana se corresponde con un día, mes y año cualquiera. Este artículo intentará guiarte en la determinación de un algoritmo que pueda resolver dicha inquietud.

Les propongo, en primer lugar, focalizarnos en un año cualquiera concreto. Pongamos, 2022. La primera pregunta para dilucidar que les propongo es la siguiente: ¿cómo determinar el día de la semana de una fecha de dicho año conociendo el día de la semana del 31 de diciembre del año anterior (en este caso 2021) que llamaremos “día base” (una suerte de día 0 del año 2022)?

El 31 de diciembre de 2021 fue viernes. Sabemos que cada 7 días volverá a ser viernes hasta la eternidad, dado que las semanas tienen 7 días. Por lo tanto, el 7 de enero de 2022, el 14 de enero de 2022, el 21 de enero de 2022 y el 28 de enero de 2022; también fueron viernes. Si los meses tuvieran todos 28 días (o 35 días o cualquier múltiplo de 7) podríamos extender esto a los siguientes meses y podríamos decir que todos los días que son múltiplos de 7 son viernes. De esta manera podría dividir el día del mes por 7 y si el residuo (o resto) de esa división es 0 (además de ser el día un múltiplo de 7) sabríamos que el día de la semana es el mismo del último día del año anterior, viernes en este caso. Pero además sabríamos que, si el residuo es 1, el día de la semana será un día después del viernes, es decir, sábado. Si el residuo es 2, es domingo y si es 6 es jueves porque 6 días después del viernes es necesariamente jueves. Pero, lamentablemente para nuestro propósito, no todos los meses tienen 28 días y por los tanto necesitamos hacer ajustes a esta primera aproximación para que funcione para los meses que le siguen a enero. Salvo febrero, en los años no bisiestos, todos los meses tienen más de 28 días. La siguiente tabla muestra la cantidad de días por encima de 28 que tiene cada mes:

Tabla 1

Sabemos entonces que, en febrero deberíamos agregar 3 días (el exceso de enero) para poder seguir la metodología de trabajar con los residuos de dividir el número del mes por 7. Por ejemplo, al 2 de febrero de 2022 le tenemos que agregar 3 días. De esta manera si al día del mes le agregamos 3 días obtenemos el número 5. El residuo de dividir el 5 entre 7 es 5, por lo tanto, sabemos que el 2 de febrero cae 5 días después que un viernes (nuestro día base). De esta manera, podemos afirmar que el 2 de febrero de 2022 fue miércoles. Si queremos hacer los mismo para el mes de marzo, no solo tenemos que agregar al día del mes el excedente de enero, sino también el de febrero y así sucesivamente para los siguientes meses hasta llegar a diciembre; para luego calcular los residuos que surjan de dividir por 7 dichos números acumulados. En resumen, cada mes (excepto enero) debería acumular el excedente acumulado de los meses previos de ese mismo año. En la Tabla 2 se agregan los excedentes acumulados de los meses anteriores a cada mes y los residuos correspondientes.

Tabla 2

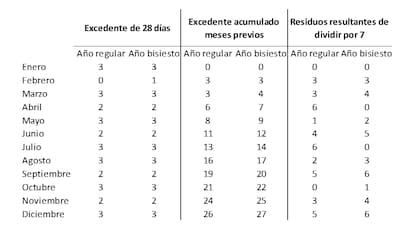
De esta manera podríamos calcular, por ejemplo, el día de la semana que corresponde al 15 de noviembre de 2022. Para tal propósito deberíamos tomar el número 15 correspondiente al día del mes, agregarle el número 3 que surge de la anteúltima columna de la Tabla 2 correspondiente a un año regular (2022 no es bisiesto) para el mes de noviembre. Obtenemos el número 18 que tiene un residuo de 4 si lo dividimos por 7. Sabemos entonces que el 15 de noviembre de 2022 es 4 días después de un viernes, es decir, un martes.

Estamos ahora en condiciones de escribir una primera versión de nuestra fórmula. Para determinar cuántos días después del día de la semana correspondiente 31 de diciembre del año anterior se ubicará cualquier día del año en curso deberé calcular el residuo de dividir por 7 al resultado de sumar el día del mes (lo llamaremos “N”) con el “código” del mes (lo llamaremos “M”) correspondiente de las últimas 2 columnas de la Tabla 2. Puesto en fórmula:

Para calcular cuántos días después del viernes cae el 24 de septiembre de 2022:

Por lo tanto, el 24 de septiembre de 2022 será 1 día después del viernes, es decir, sábado.

En definitiva, si conozco el día de la semana correspondiente al último día del mes anterior a un año cualquiera, y memorizo los códigos de la columna correspondiente para cada año en curso podría calcular mentalmente cualquier día de la semana que se corresponda a cualquier fecha de ese año en forma mental y rápida.

Si hasta acá venimos bien, podemos avanzar a la segunda parte de este artículo. Necesitamos ahora determinar el día de la semana para un día cualquiera de cualquier año.

Un primer elemento para tener en cuenta es que un año regular tiene 365 días igual a 52 x 7 + 1. Es decir que un año regular tiene 52 semanas completas y 1 día. Por lo tanto, si de un año regular a otro regular cada día del último año será 1 día de la semana después del mismo día del año anterior. Por ejemplo, el 20 de abril de 2022 fue miércoles por lo tanto el 20 de abril de 2023 será jueves. ¿Cómo podemos hacer para que cada año difiera en un día del cálculo del año anterior? Una forma sería tomar las últimas 2 cifras de cada año y calcular el residuo de su división por 7. Veamos en la Tabla 3 que efectivamente los residuos o restos de cada año son en uno mayores al resto del año inmediato anterior. Recordemos también que en nuestro “leguaje de semanas”, el número que le sigue al 6 es el 0.

Tabla 3

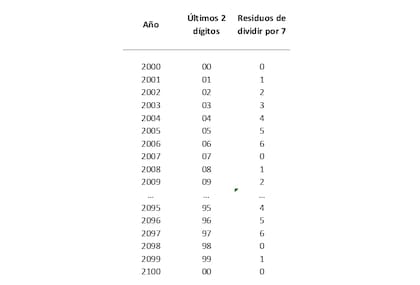
Quizá habrán notado que esto funciona a lo largo de todo el siglo XXI que tomé como ejemplo, pero la lógica se interrumpe cuando cambio de siglo en el año 2100 (en la última fila de la Tabla 3), dado que al 1 que corresponde al año 2099 le debería seguir el 2 en lugar del 0. Nos queda entonces la inquietud de cómo resolver los cambios de siglo que retomaremos en un momento. Por otro lado, dijimos que los años regulares tienen 365 días, pero los bisiestos tienen 366, por consiguiente, en principio, cada 4 años tenemos que sumar 1 día más. Para ello podríamos dividir los últimos 2 dígitos de cada año por 4 y tomar solo la parte entera del resultado. Por lo tanto, podemos seguir aproximando nuestra fórmula agregando por un lado los últimos 2 dígitos del año correspondiente (lo llamaremos “A”) y por el otro, la parte entera de la división entre los últimos 2 dígitos del año y 4. Veamos cómo quedaría la fórmula.

En este punto, me gustaría hacer un pequeño ajuste al código de los meses (M) de los años bisiestos que determinamos la última columna de la Tabla 2. Dado que en la nueva fórmula incorporamos el término ENT(A/4) que ya agrega el día adicional cada 4 años correspondiente a los años bisiestos, debemos restarle 1 día a la última columna de la Tabla 2 para compensarlo. A continuación, detallo cómo quedan los códigos de los meses (M) para los años regulares (estos no cambian) y los bisiestos que retroceden un día respecto de la Tabla 2.

Tabla 4

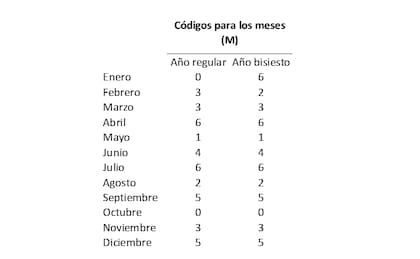
Nótese que ahora los códigos solo son diferentes para los meses de enero y febrero.

Volvamos entonces al hecho de que cuando hay un cambio de siglo queda algún ajuste por hacer, sabiendo además que queremos prescindir de un día base.

Para ver si podemos resolver estas cuestiones vamos a trabajar con algunos ejemplos. Tomemos el 31 de diciembre de 2099 y apliquemos la fórmula que trabajamos hasta el momento:

N = 31

M = 5

A = 99

ENT (A/4) = 24 ya que 99 / 4 = 24,75

N + M + A + ENT (A/4) = 31 + 5 + 99 + 24 = 159

Finalmente, el residuo de 159 / 7 = 5 porque 22 x 7 + 5 = 159

Quiere decir que 5 es el resultado de nuestra fórmula parcial.

Ahora les propongo que usemos la siguiente traducción numérica de la Tabla 5 para cada día de la semana:

Tabla 5

Podemos informarnos mirando un calendario que el 31 de diciembre de 2099 será jueves. Ahora recordemos que el resultado de nuestra fórmula nos dio 5 que se corresponde con el viernes de la Tabla 5. Por lo tanto, para ajustarlo al jueves le tendría que agregar 6 días. De esta manera puedo ajustar la fórmula de la siguiente manera:

Dicha fórmula ahora es válida para todo el siglo XXI y no necesito día base. Podemos decir que “matamos 2 pájaros de un solo tiro”. Quiere decir que el código para del siglo (que llamaremos “S”) será el 6 para el siglo XXI.

Por los tanto la fórmula general sería:

Donde nos resta saber cuál es el código para todos los demás siglos.

Para ello necesitamos antes revisar la definición de año bisiesto. Los años bisiestos son los múltiplos de 4 excepto los que son además múltiplos de 100 que no son múltiplos de 400. Por ejemplo 2020 y 2024 son bisiestos por ser múltiplos de 4 que no son múltiplos de 100. Los años 1800 y 1900 nos son bisiestos porque si bien son múltiplos de 4 son también múltiplos de 100 y no son múltiplos de 400. Los años 1600 y 2000 son bisiestos a pesar de ser múltiplos de 100 porque son también múltiplos de 400.

Volvamos ahora entonces al código del siglo (S). Para poder determinarlo trabajaremos comparando el paso del 31 de diciembre de 2099 al día siguiente, el 1 de enero de 2100 que es el primer día del siglo XXII y que obviamente sabemos que tiene que ser viernes. Veamos entonces la Tabla 6 a continuación.

Tabla 6

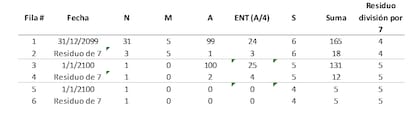
Las primeras 2 filas de la Tabla 6 tienen el cálculo del día de la semana correspondiente al 31 de diciembre de 2099 según la fórmula que ya dedujimos anteriormente. Vemos en la última columna de cualquiera de dichas filas que el resultado corresponde al jueves. Para pasar al año siguiente, “A” debería valer 100 para agregar el residuo de dividir los 365 días de 2099 por 7. Por consiguiente, en la fórmula correspondiente al 1 de enero de 2100 en las filas 3 y 4 reemplacé “A” por 100 y “ENT (A/4)” por 100/4 = 25. Adicionalmente como el año 2100 es un múltiplo de 4 en la columna ENT (A/4) ya calcula el día adicional por ser supuestamente bisiesto. Sin embargo, dijimos que si además de múltiplo de 4 es múltiplo de 100 que no es múltiplo de 400, entonces no es bisiesto. Por ese motivo del código de siglo del siglo XXI resto 1 para recuperar ese día agregado de más en la columna anterior. De ahí que en las filas 3 y 4 correspondientes a la columna “S” agregué un 5 resultante de restar en 1 el código del siglo XXI que es 6. Con estos ajustes vemos en la última columna de las filas 3 y 4 que el resultado se corresponde con el viernes que obviamente le sigue al jueves del día anterior. Pero como para ingresar el año no usamos las últimas 3 cifras sino las últimas 2, necesitamos seguir haciendo refinamientos. Para ello trabajaremos con las filas 5 y 6 de la Tabla 6. Como vimos en la Tabla 3, cuando hay un cambio de siglo, nuestra fórmula, en lugar de agregar 1 día, retrocede 1 al tomar el residuo de las últimas dos cifras del año correspondiente. Con lo cual tenemos que agregar 2 días cada vez que hay un cambio de siglo para compensar dicho efecto. Pero, además, el residuo de dividir por 7 el resultado de la división entre 100 y 4 resulta ser 4 (porque 100 / 4 = 25 y el residuo de dividirlo entre 7 es 4) pero cuando dividimos por 4 los últimos 2 dígitos del año correspondiente el resultado para el primer año del nuevo siglo también nos da 0.

Por ende, debemos agregar otros 4 días para también compensarlos. Un total de 6 días que son los que están en la fila 4 de la Tabla 6 en las columnas “A” y “ENT (A/4)”. Voy a usar el código de siglo “S” para hacer esa compensación. Por lo tanto, dichos 6 días a compensar, se los sumo a los 5 que habíamos determinado en la columna “S” de las filas 3 y 4. De esta manera obtenemos el número 11 y el residuo de dividirlo por 7 es 4 que resulta ser el código correspondiente al siglo XXII y que lo incorporé en las filas 5 y 6 de la columna “S” de la Tabla 6. Por lo tanto, si para pasar del siglo XXI al siglo XXII en código de siglo pasa de 6 a 4, entonces en cada cambio de siglo hay que ajustar el código del siglo restándole 2 días al código correspondiente al siglo anterior. De esta forma el código del siglo XXIII será 2 y el del XXIV es 0. Cuando llegamos al siglo XXV estamos en el año 2400 y resulta que a pesar de ser múltiplo de 100 también es múltiplo de 400 y es entonces bisiesto. Por lo tanto, debemos volver a agregar el día que sacamos. Esto hace que en lugar de restar 2, esta vez restamos solo 1 pasando de 0 a -1 que en nuestro lenguaje de residuos de dividir por 7 equivale a 6, y el ciclo vuelve a empezar. Veamos entonces en la siguiente Tabla 7 los códigos de siglo (S) que acabamos de determinar resaltados en gris y como la secuencia se repite para adelante y para atrás en el tiempo:

Tabla 7

De esta manera en las Tablas 4 y 7 tenemos los elementos para reemplazar en la fórmula general y obtener el número de la Tabla 5 que se corresponde con el día de la semana que se pretende calcular para una fecha cualquiera.

Para cerrar incluyo varios ejemplos luego de repetir la fórmula general que nos permitirá obtener el día de la semana correspondiente a una fecha dada:

Ejemplos:

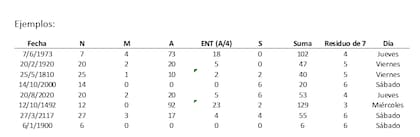
La primera fecha es el día de mi nacimiento, también incorporé el día de la Revolución de Mayo y el descubrimiento de América.

Con relación a la última fecha, me parece curioso destacar que el programa Excel de Microsoft calcula el día de la semana para una fecha dada a través de la fórmula DIASEM. Las fechas disponibles en Excel son a partir del 1 de enero de 1900. Sin embargo, los días de la semana que arroja desde el 1 de enero de 1900 hasta el 29 de febrero de 1900 son incorrectos, al menos en mi versión. De hecho, según el Excel, existió el 29 de febrero de 1900 pero 1900 no es un año bisiesto por ser múltiplo de 100 y no de 400. Este error genera, a mi entender, el error del cálculo de los días de la semana en los días previos al 29 de febrero de 1900. Puntualmente en mi ejemplo, según el Excel, el 6 de enero de 1900 fue viernes cuando en realidad fue sábado.

Conforme a los criterios de

Tipo de trabajo:

noticia original

Conocé más

Test viral. Elegí una fruta y conocé tu verdadera personalidad

Test matemático. Tres ejercicios para poner a prueba tu nivel de inteligencia

Test visual. Elegí uno de estos símbolos y descubrí qué tan amable sos